Maximum A Posteriori Machine Learning

Maximum A Posteriori Machine Learning. Outline 1 introduction a rst solution example. Density estimation is the problem of estimating the probability distribution for a sample of observations from a problem domain.

PPT Introduction to Machine Learning PowerPoint Presentation ID2225024 from www.slideserve.com

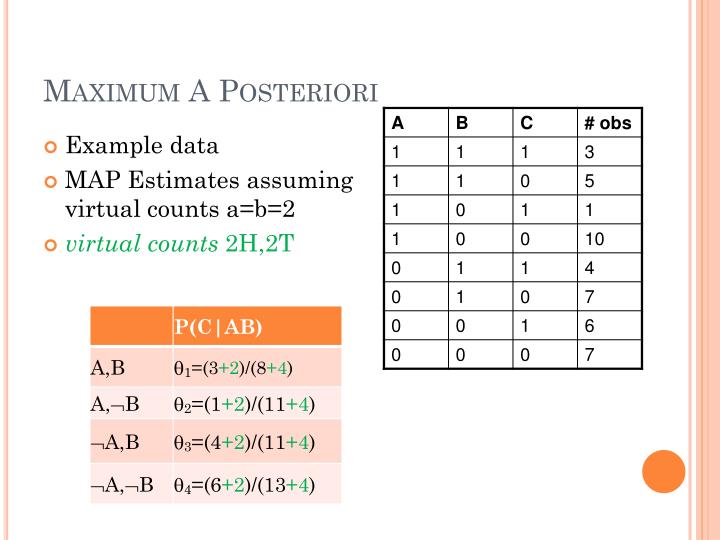
As we saw in the video lecture, the problem that we need to solve to find the maximum a posteriori estimate is when the prior of the weights is a zero mean gaussian with precision. Outline 1 introduction a rst solution example. We will select the class which maximizes.

Source: www.slideserve.com

2 days agolast year, mit researchers announced that they had built “liquid” neural networks, inspired by the brains of small species: Outline 1 introduction a rst solution example.

Source: www.youtube.com

We will select the class which maximizes. As we saw in the video lecture, the problem that we need to solve to find the maximum a posteriori estimate is when the prior of the weights is a zero mean gaussian with precision.

In Bayesian Statistics, A Maximum A Posteriori Probability Estimate Is An Estimate Of An Unknown Quantity, That Equals The Mode Of The Posterior Distribution.

The method is often used to estimate the parameters of a probabilistic. Note that the evidence ∑ θ p ( d | θ) p ( θ) can in fact be. Density estimation is the problem of estimating the probability distribution for a sample of observations from a problem domain.

Outline 1 Introduction A Rst Solution Example.

The map can be used to. A class of flexible, robust machine learning models. We have the prior, we have the likelihood.

Maximum Likelihood Estimation (Mle) Last Modified December 24, 2017.

Maximum a posteriori (map) estimation. We now have to compute the posterior. Typically, estimating the entire distribution is intractable, and instead, we are happy to have the expected value of the distribution, such as the mean or mode.

Θ ∗ = Arg Max Θ P ( Θ | D).

We use something called maximum a posteriori estimation. Maximum a posteriori estimation (map) maximum a posteriori estimation, as is stated in its name, maximizes the posterior probability $p(a | b)$ in bayes’ theorem with. Here, a level of 15 mg/l is collected at 22 h after the first dose.

As We Saw In The Video Lecture, The Problem That We Need To Solve To Find The Maximum A Posteriori Estimate Is When The Prior Of The Weights Is A Zero Mean Gaussian With Precision.

Maximum a posteriori estimation is used in data science and machine learning to estimate the parameters of a model. Typically, estimating the entire distribution is. 2 days agolast year, mit researchers announced that they had built “liquid” neural networks, inspired by the brains of small species: